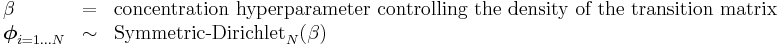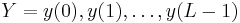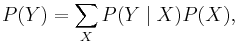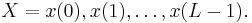Hidden Markov model

A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved (hidden) states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E. Baum and coworkers.^[1]^[2]^[3]^[4]^[5]

In a regular Markov model, the state is directly visible to the observer, and therefore the state transition probabilities are the only parameters. In a hidden Markov model, the state is not directly visible, but output, dependent on the state, is visible. Each state has a probability distribution over the possible output tokens. Therefore the sequence of tokens generated by an HMM gives some information about the sequence of states. Note that the adjective 'hidden' refers to the state sequence through which the model passes, not to the parameters of the model; even if the model parameters are known exactly, the model is still 'hidden'.

Hidden Markov models are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition,^[6] part-of-speech tagging, musical score following,^[7] partial discharges^[8] and bioinformatics.

A hidden Markov model can be considered a generalization of a mixture model where the hidden variables (or latent variables), which control the mixture component to be selected for each observation, are related through a Markov process rather than independent of each other.

Description in terms of urns

In its discrete form, a hidden Markov process can be visualized as a generalization of the Urn problem. For instance:^[9] A genie is in a room that is not visible to an observer. The genie is drawing balls labeled y1, y2, y3, ... from the urns X1, X2, X3, ... in that room and putting the balls onto a conveyor belt, where the observer can observe the sequence of the balls but not the sequence of urns from which they were drawn. The genie has some procedure to choose urns; the choice of the urn for the n-th ball depends upon only a random number and the choice of the urn for the (n − 1)-th ball. The choice of urn does not directly depend on the urns further previous, therefore this is called a Markov process. It can be described by the upper part of Figure 1.

The Markov process itself cannot be observed, and only the sequence of labeled balls can be observed, thus this arrangement is called a "hidden Markov process". This is illustrated by the lower part of the diagram shown in Figure 1, where one can see that balls y1, y2, y3, y4 can be drawn at each state. Even if the observer knows the composition of the urns and has just observed a sequence of three balls, e.g. y1, y2 and y3 on the conveyor belt, the observer still cannot be sure which urn (i.e., at which state) the genie has drawn the third ball from. However, the observer can work out other details, such as the identity of the urn the genie is most likely to have drawn the third ball from.

Architecture of a hidden Markov model

The diagram below shows the general architecture of an instantiated HMM. Each oval shape represents a random variable that can adopt any of a number of values. The random variable x(t) is the hidden state at time t (with the model from the above diagram, x(t) ∈ { x₁, x₂, x₃ }). The random variable y(t) is the observation at time t (with y(t) ∈ { y₁, y₂, y₃, y₄ }). The arrows in the diagram (often called a trellis diagram) denote conditional dependencies.

From the diagram, it is clear that the conditional probability distribution of the hidden variable x(t) at time t, given the values of the hidden variable x at all times, depends only on the value of the hidden variable x(t − 1): the values at time t − 2 and before have no influence. This is called the Markov property. Similarly, the value of the observed variable y(t) only depends on the value of the hidden variable x(t) (both at time t).

In the standard type of hidden Markov model considered here, the state space of the hidden variables is discrete, while the observations themselves can either be discrete (typically generated from a categorical distribution) or continuous (typically from a Gaussian distribution). The parameters of a hidden Markov model are of two types, transition probabilities and emission probabilities (also known as output probabilities). The transition probabilities control the way the hidden state at time $t$ is chosen given the hidden state at time $t-1$ .

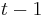The hidden state space is assumed to consist of one of $N$ possible values, modeled as a categorical distribution. 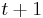(See the section below on extensions for other possibilities.) This means that for each of the $N$ possible states that a hidden variable at time $t$ can be in, there is a transition probability from this state to each of the $N$ possible states of the hidden variable at time $t%2B1$ , for a total of $N^2$ transition probabilities. 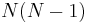(Note, however, that the set of transition probabilities for transitions from any given state must sum to 1, meaning that any one transition probability can be determined once the others are known, leaving a total of $N(N-1)$ transition parameters.)

In addition, for each of the $N$ possible states, there is a set of emission probabilities governing the distribution of the observed variable at a particular time given the state of the hidden variable at that time. The size of this set depends on the nature of the observed variable. 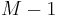For example, if the observed variable is discrete with $M$ possible values, governed by a categorical distribution, there will be $M-1$ separate parameters, for a total of 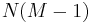$N(M-1)$ emission parameters over all hidden states. 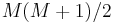On the other hand, if the observed variable is an $M$ -dimensional vector distributed according to an arbitrary multivariate Gaussian distribution, there will be $M$ parameters controlling the means and $M(M%2B1)/2$ parameters controlling the covariance matrix, for a total of 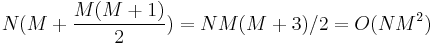$N(M %2B \frac{M(M%2B1)}{2}) = NM(M%2B3)/2 = O(NM^2)$ emission parameters. (In such a case, unless the value of $M$ is small, it may be more practical to restrict the nature of the covariances between individual elements of the observation vector, e.g. by assuming that the elements are independent of each other, or less restrictively, are independent of all but a fixed number of adjacent elements.)

Mathematical description of a hidden Markov model

General description

A basic, non-Bayesian hidden Markov model can be described as follows:

$\begin{array}{lcl} N &=& \text{number of states} \\ T &=& \text{number of observations} \\ \theta_{i=1 \dots N} &=& \text{emission parameter for an observation associated with state } i \\ \phi_{i=1 \dots N, j=1 \dots N} &=& \text{probability of transition from state } i \text{ to state } j \\ \boldsymbol\phi_{i=1 \dots N} &=& N\text{-dimensional vector, composed of } \phi_{i,1 \dots N} \text{; must sum to 1} \\ x_{t=1 \dots T} &=& \text{state of observation at time } t \\ y_{t=1 \dots T} &=& \text{observation at time } t \\ F(y|\theta) &=& \text{probability distribution of an observation, parametrized on } \theta \\ x_{t=2 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}}) \\ y_{t=1 \dots T} &\sim& F(\theta_{x_t}) \end{array}$

Note that, in the above model (and also the one below), the prior distribution of the initial state 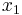$x_1$ is not specified. Typical learning models correspond to assuming a discrete uniform distribution over possible states (i.e. no particular prior distribution is assumed).

In a Bayesian setting, all parameters are associated with random variables, as follows:

$\begin{array}{lcl} N,T &=& \text{as above} \\ \theta_{i=1 \dots N}, \phi_{i=1 \dots N, j=1 \dots N}, \boldsymbol\phi_{i=1 \dots N} &=& \text{as above} \\ x_{t=1 \dots T}, y_{t=1 \dots T}, F(y|\theta) &=& \text{as above} \\ \alpha &=& \text{shared hyperparameter for emission parameters} \\ \beta &=& \text{shared hyperparameter for transition parameters} \\ H(\theta|\alpha) &=& \text{prior probability distribution of emission parameters, parametrized on } \alpha \\ \theta_{i=1 \dots N} &\sim& H(\alpha) \\ \boldsymbol\phi_{i=1 \dots N} &\sim& \operatorname{Symmetric-Dirichlet}_N(\beta) \\ x_{t=2 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi_{x_{i-t}}) \\ y_{t=1 \dots T} &\sim& F(\theta_{x_t}) \end{array}$

These characterizations use $F$ and $H$ to describe arbitrary distributions over observations and parameters, respectively. Typically $H$ will be the conjugate prior of $F$ . The two most common choices of $F$ are Gaussian and categorical; see below.

Compared with a simple mixture model

As mentioned above, the distribution of each observation in a hidden Markov model is a mixture density, with the states of the HMM corresponding to mixture components. It is useful to compare the above characterizations for an HMM with the corresponding characterizations, of a mixture model, using the same notation.

A non-Bayesian mixture model:

$\begin{array}{lcl} N &=& \text{number of mixture components} \\ T &=& \text{number of observations} \\ \theta_{i=1 \dots N} &=& \text{parameter of distribution of observation associated with component } i \\ \phi_{i=1 \dots N} &=& \text{mixture weight, i.e. prior probability of a particular component } i \\ \boldsymbol\phi &=& N\text{-dimensional vector composed of all the individual } \phi_{1 \dots N} \text{; must sum to 1} \\ x_{i=1 \dots T} &=& \text{component of observation } i \\ y_{i=1 \dots T} &=& \text{observation } i \\ F(y|\theta) &=& \text{probability distribution of an observation, parametrized on } \theta \\ x_{i=1 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi) \\ y_{i=1 \dots T} &\sim& F(\theta_{x_i}) \end{array}$

A Bayesian mixture model:

$\begin{array}{lcl} N,T &=& \text{as above} \\ \theta_{i=1 \dots N}, \phi_{i=1 \dots N}, \boldsymbol\phi &=& \text{as above} \\ x_{i=1 \dots T}, y_{i=1 \dots T}, F(y|\theta) &=& \text{as above} \\ \alpha &=& \text{shared hyperparameter for component parameters} \\ \beta &=& \text{shared hyperparameter for mixture weights} \\ H(\theta|\alpha) &=& \text{prior probability distribution of component parameters, parametrized on } \alpha \\ \theta_{i=1 \dots N} &\sim& H(\alpha) \\ \boldsymbol\phi &\sim& \operatorname{Symmetric-Dirichlet}_N(\beta) \\ x_{i=1 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi) \\ y_{i=1 \dots T} &\sim& F(\theta_{x_i}) \end{array}$

Examples of HMMs

The following mathematical descriptions are fully written out and explained, for ease of implementation.

A typical non-Bayesian HMM with Gaussian observations looks like this:

A typical Bayesian HMM with Gaussian observations looks like this:

$\begin{array}{lcl} N &=& \text{number of states} \\ T &=& \text{number of observations} \\ \phi_{i=1 \dots N, j=1 \dots N} &=& \text{probability of transition from state } i \text{ to state } j \\ \boldsymbol\phi_{i=1 \dots N} &=& N\text{-dimensional vector, composed of } \phi_{i,1 \dots N} \text{; must sum to 1} \\ \mu_{i=1 \dots N} &=& \text{mean of observations associated with state } i \\ \sigma^2_{i=1 \dots N} &=& \text{variance of observations associated with state } i \\ x_{t=1 \dots T} &=& \text{state of observation at time } t \\ y_{t=1 \dots T} &=& \text{observation at time } t \\ \beta &=& \text{concentration hyperparameter controlling the density of the transition matrix} \\ \mu_0, \lambda &=& \text{shared hyperparameters of the means for each state} \\ \nu, \sigma_0^2 &=& \text{shared hyperparameters of the variances for each state} \\ \boldsymbol\phi_{i=1 \dots N} &\sim& \operatorname{Symmetric-Dirichlet}_N(\beta) \\ x_{t=2 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}}) \\ \mu_{i=1 \dots N} &\sim& \mathcal{N}(\mu_0, \lambda\sigma_i^2) \\ \sigma_{i=1 \dots N}^2 &\sim& \operatorname{Inverse-Gamma}(\nu, \sigma_0^2) \\ y_{t=1 \dots T} &\sim& \mathcal{N}(\mu_{x_t}, \sigma_{x_t}^2) \end{array}$

A typical non-Bayesian HMM with categorical observations looks like this:

$\begin{array}{lcl} N &=& \text{number of states} \\ T &=& \text{number of observations} \\ \phi_{i=1 \dots N, j=1 \dots N} &=& \text{probability of transition from state } i \text{ to state } j \\ \boldsymbol\phi_{i=1 \dots N} &=& N\text{-dimensional vector, composed of } \phi_{i,1 \dots N} \text{; must sum to 1} \\ V &=& \text{dimension of categorical observations, e.g. size of word vocabulary} \\ \theta_{i=1 \dots N, j=1 \dots V} &=& \text{probability for state } i \text{ of observing the } j\text{th item} \\ \boldsymbol\theta_{i=1 \dots N} &=& V\text{-dimensional vector, composed of }\theta_{i,1 \dots V} \text{; must sum to 1} \\ x_{t=1 \dots T} &=& \text{state of observation at time } t \\ y_{t=1 \dots T} &=& \text{observation at time } t \\ x_{t=2 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}}) \\ y_{t=1 \dots T} &\sim& \text{Categorical}(\boldsymbol\theta_{x_t}) \end{array}$

A typical Bayesian HMM with categorical observations looks like this:

$\begin{array}{lcl} N &=& \text{number of states} \\ T &=& \text{number of observations} \\ \phi_{i=1 \dots N, j=1 \dots N} &=& \text{probability of transition from state } i \text{ to state } j \\ \boldsymbol\phi_{i=1 \dots N} &=& N\text{-dimensional vector, composed of } \phi_{i,1 \dots N} \text{; must sum to 1} \\ V &=& \text{dimension of categorical observations, e.g. size of word vocabulary} \\ \theta_{i=1 \dots N, j=1 \dots V} &=& \text{probability for state } i \text{ of observing the } j\text{th item} \\ \boldsymbol\theta_{i=1 \dots N} &=& V\text{-dimensional vector, composed of }\theta_{i,1 \dots V} \text{; must sum to 1} \\ x_{t=1 \dots T} &=& \text{state of observation at time } t \\ y_{t=1 \dots T} &=& \text{observation at time } t \\ \alpha &=& \text{shared concentration hyperparameter of } \boldsymbol\theta \text{ for each state} \\ \beta &=& \text{concentration hyperparameter controlling the density of the transition matrix} \\ \boldsymbol\phi_{i=1 \dots N} &\sim& \operatorname{Symmetric-Dirichlet}_N(\beta) \\ \boldsymbol\theta_{1 \dots V} &\sim& \text{Symmetric-Dirichlet}_V(\alpha) \\ x_{t=2 \dots T} &\sim& \operatorname{Categorical}(\boldsymbol\phi_{x_{t-1}}) \\ y_{t=1 \dots T} &\sim& \text{Categorical}(\boldsymbol\theta_{x_t}) \end{array}$

Note that in the above Bayesian characterizations, $\beta$ (a concentration parameter) controls the density of the transition matrix. That is, with a high value of $\beta$ (significantly above 1), the probabilities controlling the transition out of a particular state will all be similar, meaning there will be a significantly probability of transitioning to any of the other states. In other words, the path followed by the Markov chain of hidden states will be highly random. With a low value of $\beta$ (significantly below 1), only a small number of the possible transitions out of a given state will have significant probability, meaning that the path followed by the hidden states will be somewhat predictable.

A two-level Bayesian HMM

An alternative for the above two Bayesian examples would be to add another level of prior parameters for the transition matrix. That is, replace the lines

$\begin{array}{lcl} \beta &=& \text{concentration hyperparameter controlling the density of the transition matrix} \\ \boldsymbol\phi_{i=1 \dots N} &\sim& \operatorname{Symmetric-Dirichlet}_N(\beta) \end{array}$

with the following:

$\begin{array}{lcl} \gamma &=& \text{concentration hyperparameter controlling how many states are intrinsically likely} \\ \beta &=& \text{concentration hyperparameter controlling the density of the transition matrix} \\ \boldsymbol\eta &=& N\text{-dimensional vector of probabilities, specifying the intrinsic probability of a given state} \\ \boldsymbol\eta &\sim& \operatorname{Symmetric-Dirichlet}_N(\gamma) \\ \boldsymbol\phi_{i=1 \dots N} &\sim& \operatorname{Dirichlet}_N(\beta N \boldsymbol\eta) \end{array}$

What this means is the following:

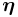$\boldsymbol\eta$ is a probability distribution over states, specifying which states are inherently likely. The greater the probability of a given state in this vector, the more likely is a transition to that state (regardless of the starting state).
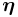$\gamma$ controls the density of $\boldsymbol\eta$ . Values significantly above 1 cause a dense vector where all states will have similar prior probabilities. Values significantly below 1 cause a sparse vector where only a few states are inherently likely (have prior probabilities significantly above 0).
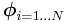$\beta$ controls the density of the transition matrix, or more specifically, the density of the N different probability vectors $\boldsymbol\phi_{i=1 \dots N}$ specifying the probability of transitions out of state i to any other state.

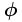Imagine that the value of $\beta$ is significantly above 1. Then the different $\boldsymbol\phi$ vectors will be dense, i.e. the probability mass will be spread out fairly evenly over all states. However, to the extent that this mass is unevenly spread, 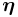$\boldsymbol\eta$ controls which states are likely to get more mass than others.

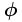Now, imagine instead that $\beta$ is significantly below 1. This willl make the $\boldsymbol\phi$ vectors sparse, i.e. almost all the probability mass is distributed over a small number of states, and for the rest, a transition to that state will be very unlikely. Notice that there are different 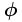$\boldsymbol\phi$ vectors for each starting state, and so even if all the vectors are sparse, different vectors may distribute the mass to different ending states. However, for all of the vectors, 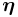$\boldsymbol\eta$ controls which ending states are likely to get mass assigned to them. 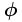For example, if $\beta$ is 0.1, then each $\boldsymbol\phi$ will be sparse and, for any given starting state i, the set of states 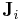$\mathbf{J}_i$ to which transitions are likely to occur will be very small, typically having only one or two members. Now, if the probabilities in 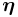$\boldsymbol\eta$ are all the same (or equivalently, one of the above models without 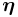$\boldsymbol\eta$ is used), then for different i, there will be different states in the corresponding 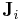$\mathbf{J}_i$ , so that all states are equally likely to occur in any given 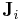$\mathbf{J}_i$ . On the other hand, if the values in 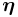$\boldsymbol\eta$ are unbalanced, so that one state has a much higher probability than others, almost all 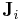$\mathbf{J}_i$ will contain this state; hence, regardless of the starting state, transitions will nearly always occur to this given state.

Hence, a two-level model such as just described allows independent control over (1) the overall density of the transition matrix, and (2) the density of states to which transitions are likely (i.e. the density of the prior distribution of states in any particular hidden variable $x_i$ ). In both cases this is done while still assuming ignorance over which particular states are more likely than others. 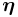If it is desired to inject this information into the model, the probability vector $\boldsymbol\eta$ can be directly specified; or, if there is less certainty about these relative probabilities, a non-symmetric Dirichlet distribution can be used as the prior distribution over 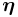$\boldsymbol\eta$ . That is, instead of using a symmetric Dirichlet distribution with a single parameter $\gamma$ (or equivalently, a general Dirichlet with a vector all of whose values are equal to $\gamma$ ), use a general Dirichlet with values that are variously greater or less than $\gamma$ , according to which state is more or less preferred.

Learning

The parameter learning task in HMMs is to find, given an output sequence or a set of such sequences, the best set of state transition and output probabilities. The task is usually to derive the maximum likelihood estimate of the parameters of the HMM given the set of output sequences. No tractable algorithm is known for solving this problem exactly, but a local maximum likelihood can be derived efficiently using the Baum–Welch algorithm or the Baldi–Chauvin algorithm. The Baum–Welch algorithm is an example of a forward-backward algorithm, and is a special case of the expectation-maximization algorithm.

Inference

Several inference problems are associated with hidden Markov models, as outlined below.

Filtering

The task is to compute, given the model's parameters and a sequence of observations, the distribution over hidden states at the end of the sequence, i.e. to compute 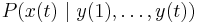$P(x(t)\ |\ y(1),\dots,y(t))$ . This problem can be handled efficiently using the forward algorithm.

Probability of an observed sequence

The task is to compute, given the parameters of the model, the probability of a particular output sequence. This requires summation over all possible state sequences:

The probability of observing a sequence

$Y=y(0), y(1),\dots,y(L-1)\,$

of length L is given by

$P(Y)=\sum_{X}P(Y\mid X)P(X),\,$

where the sum runs over all possible hidden-node sequences

$X=x(0), x(1), \dots, x(L-1).\,$

Applying the principle of dynamic programming, this problem, too, can be handled efficiently using the forward algorithm.

Most likely explanation

The task is to compute, given the parameters of the model and a particular output sequence, the state sequence that is most likely to have generated that output sequence (see illustration on the right). This requires finding a maximum over all possible state sequences, but can similarly be solved efficiently by the Viterbi algorithm.

Smoothing

The task is to compute, given the parameters of the model and a particular output sequence up to time $t$ , the probability distribution over hidden states for a point in time in the past, i.e. to compute 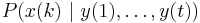$P(x(k)\ |\ y(1), \dots, y(t))$ for some 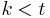$k < t$ . The forward-backward algorithm is an efficient method for computing the smoothed values for all hidden state variables.

Statistical significance

For some of the above problems, it may also be interesting to ask about statistical significance. What is the probability that a sequence drawn from some null distribution will have an HMM probability (in the case of the forward algorithm) or a maximum state sequence probability (in the case of the Viterbi algorithm) at least as large as that of a particular output sequence?^[10] When an HMM is used to evaluate the relevance of a hypothesis for a particular output sequence, the statistical significance indicates the false positive rate associated with accepting the hypothesis for the output sequence.

A concrete example

Consider two friends, Alice and Bob, who live far apart from each other and who talk together daily over the telephone about what they did that day. Bob is only interested in three activities: walking in the park, shopping, and cleaning his apartment. The choice of what to do is determined exclusively by the weather on a given day. Alice has no definite information about the weather where Bob lives, but she knows general trends. Based on what Bob tells her he did each day, Alice tries to guess what the weather must have been like.

Alice believes that the weather operates as a discrete Markov chain. There are two states, "Rainy" and "Sunny", but she cannot observe them directly, that is, they are hidden from her. On each day, there is a certain chance that Bob will perform one of the following activities, depending on the weather: "walk", "shop", or "clean". Since Bob tells Alice about his activities, those are the observations. The entire system is that of a hidden Markov model (HMM).

Alice knows the general weather trends in the area, and what Bob likes to do on average. In other words, the parameters of the HMM are known. They can be represented as follows in the Python programming language:

states = ('Rainy', 'Sunny')
 
observations = ('walk', 'shop', 'clean')
 
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
 
transition_probability = {
   'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
   'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
   }
 
emission_probability = {
   'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
   'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
   }

In this piece of code, start_probability represents Alice's belief about which state the HMM is in when Bob first calls her (all she knows is that it tends to be rainy on average). The particular probability distribution used here is not the equilibrium one, which is (given the transition probabilities) approximately {'Rainy': 0.57, 'Sunny': 0.43}. The transition_probability represents the change of the weather in the underlying Markov chain. In this example, there is only a 30% chance that tomorrow will be sunny if today is rainy. The emission_probability represents how likely Bob is to perform a certain activity on each day. If it is rainy, there is a 50% chance that he is cleaning his apartment; if it is sunny, there is a 60% chance that he is outside for a walk.

This example is further elaborated in the Viterbi algorithm page.

Applications of hidden Markov models

HMMs can be applied in many fields where the goal is to recover a data sequence that is not immediately observable (but other data that depends on the sequence is). Applications include:

History

Hidden Markov Models were first described in a series of statistical papers by Leonard E. Baum and other authors in the second half of the 1960s. One of the first applications of HMMs was speech recognition, starting in the mid-1970s.^[12]^[13]^[14]^[15]

In the second half of the 1980s, HMMs began to be applied to the analysis of biological sequences,^[16] in particular DNA. Since then, they have become ubiquitous in the field of bioinformatics.^[17]

Types of hidden Markov models

Hidden Markov models can model complex Markov processes where the states emit the observations according to some probability distribution. One such example of distribution is Gaussian distribution, in such a Hidden Markov Model the states output is represented by a Gaussian distribution.

Moreover it could represent even more complex behavior when the output of the states is represented as mixture of two or more Gaussians, in which case the probability of generating an observation is the product of the probability of first selecting one of the Gaussians and the probability of generating that observation from that Gaussian.

Extensions

In the hidden Markov models considered above, the state space of the hidden variables is discrete, while the observations themselves can either be discrete (typically generated from a categorical distribution) or continuous (typically from a Gaussian distribution). Hidden Markov models can also be generalized to allow continuous state spaces. Examples of such models are those where the Markov process over hidden variables is a linear dynamical system, with a linear relationship among related variables and where all hidden and observed variables follow a Gaussian distribution. In simple cases, such as the linear dynamical system just, exact inference is tractable (in this case, using the Kalman filter); however, in general, exact inference in HMMs with continuous latent variables is infeasible, and approximate methods must be used, such as the extended Kalman filter or the particle filter.

Hidden Markov models are generative models, in which the joint distribution of observations and hidden states, or equivalently both the prior distribution of hidden states (the transition probabilities) and conditional distribution of observations given states (the emission probabilities), is modeled. The above algorithms implicitly assume a uniform prior distribution over the transition probabilities. However, it is also possible to create hidden Markov models with other types of prior distributions. An obvious candidate, given the categorical distribution of the transition probabilities, is the Dirichlet distribution, which is the conjugate prior distribution of the categorical distribution. Typically, a symmetric Dirichlet distribution is chosen, reflecting ignorance about which states are inherently more likely than others. The single parameter of this distribution (termed the concentration parameter) controls the relative density or sparseness of the resulting transition matrix. A choice of 1 yields a uniform distribution. Values greater than 1 produce a dense matrix, in which the transition probabilities between pairs of states are likely to be nearly equal. Values less than 1 result in a sparse matrix in which, for each given source state, only a small number of destination states have non-negligible transition probabilities. It is also possible to use a two-level prior Dirichlet distribution, in which one Dirichlet distribution (the upper distribution) governs the parameters of another Dirichlet distribution (the lower distribution), which in turn governs the transition probabilities. The upper distribution governs the overall distribution of states, determining how likely each state is to occur; its concentration parameter determines the density or sparseness of states. Such a two-level prior distribution, where both concentration parameters are set to produce sparse distributions, might be useful for example in unsupervised part-of-speech tagging, where some parts of speech occur much more commonly than others; learning algorithms that assume a uniform prior distribution generally perform poorly on this task. The parameters of models of this sort, with non-uniform prior distributions, can be learned using Gibbs sampling or extended versions of the expectation-maximization algorithm.

An extension of the previously-described hidden Markov models with Dirichlet priors uses a Dirichlet process in place of a Dirichlet distribution. This type of model allows for an unknown and potentially infinite number of states. It is common to use a two-level Dirichlet process, similar to the previously-described model with two levels of Dirichlet distributions. Such a model is called a hierarchical Dirichlet process hidden Markov model, or HDP-HMM for short.

A different type of extension uses a discriminative model in place of the generative model of standard HMM's. This type of model directly models the conditional distribution of the hidden states given the observations, rather than modeling the joint distribution. An example of this model is the so-called maximum entropy Markov model (MEMM), which models the conditional distribution of the states using logistic regression (also known as a "maximum entropy model"). The advantage of this type of model is that arbitrary features (i.e. functions) of the observations can be modeled, allowing domain-specific knowledge of the problem at hand to be injected into the model. Models of this sort are not limited to modeling direct dependencies between a hidden state and its associated observation; rather, features of nearby observations, of combinations of the associated observation and nearby observations, or in fact of arbitrary observations at any distance from a given hidden state can be included in the process used to determine the value of a hidden state. Furthermore, there is no need for these features to be statistically independent of each other, as would be the case if such features were used in a generative model. Finally, arbitrary features over pairs of adjacent hidden states can be used rather than simple transition probabilities. The disadvantages of such models are: (1) The types of prior distributions that can be placed on hidden states are severely limited; (2) It is not possible to predict the probability of seeing an arbitrary observation. This second limitation is often not an issue in practice, since many common usages of HMM's do not require such predictive probabilities.

A variant of the previously described discriminative model is the linear-chain conditional random field. This uses an undirected graphical model (aka Markov random field) rather than the directed graphical models of MEMM's and similar models. The advantage of this type of model is that it does not suffer from the so-called label bias problem of MEMM's, and thus may make more accurate predictions. The disadvantage is that training can be slower than for MEMM's.

Yet another variant is the factorial hidden Markov model, which allows for a single observation to be conditioned on the corresponding hidden variables of a set of $K$ independent Markov chains, rather than a single Markov chain. Learning in such a model is difficult, as dynamic-programming techniques can no longer be used to find an exact solution ; in practice, approximate techniques must be used.^[18]

All of the above models can be extended to allow for more distant dependencies among hidden states, e.g. allowing for a given state to be dependent on the previous two or three states rather than a single previous state; i.e. the transition probabilities are extended to encompass sets of three or four adjacent states (or in general $K$ adjacent states). 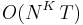The disadvantage of such models is that dynamic-programming algorithms for training them have an $O(N^K \, T)$ running time, for $K$ adjacent states and $T$ total observations (i.e. a length- $T$ Markov chain).

References

^ Baum, L. E.; Petrie, T. (1966). "Statistical Inference for Probabilistic Functions of Finite State Markov Chains". The Annals of Mathematical Statistics 37 (6): 1554–1563. doi:10.1214/aoms/1177699147. http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?handle=euclid.aoms/1177699147&view=body&content-type=pdf_1. Retrieved 28 November 2011.
^ Baum, L. E.; Eagon, J. A. (1967). "An inequality with applications to statistical estimation for probabilistic functions of Markov processes and to a model for ecology". Bulletin of the American Mathematical Society 73 (3): 360. doi:10.1090/S0002-9904-1967-11751-8. edit
^ Baum, L. E.; Sell, G. R. (1968). "Growth transformations for functions on manifolds". Pacific Journal of Mathematics 27 (2): 211–227. http://www.scribd.com/doc/6369908/Growth-Functions-for-Transformations-on-Manifolds. Retrieved 28 November 2011.
^ Baum, L. E.; Petrie, T.; Soules, G.; Weiss, N. (1970). "A Maximization Technique Occurring in the Statistical Analysis of Probabilistic Functions of Markov Chains". The Annals of Mathematical Statistics 41: 164. doi:10.1214/aoms/1177697196. edit
^ Baum, L.E. (1972). "An Inequality and Associated Maximization Technique in Statistical Estimation of Probabilistic Functions of a Markov Process". Inequalities 3: 1–8.
^ Thad Starner, Alex Pentland. Real-Time American Sign Language Visual Recognition From Video Using Hidden Markov Models. Master's Thesis, MIT, Feb 1995, Program in Media Arts
^ B. Pardo and W. Birmingham. Modeling Form for On-line Following of Musical Performances. AAAI-05 Proc., July 2005.
^ Satish L, Gururaj BI (April 2003). "Use of hidden Markov models for partial discharge pattern classification". IEEE Transactions on Dielectrics and Electrical Insulation.
^ Lawrence R. Rabiner (February 1989). "A tutorial on Hidden Markov Models and selected applications in speech recognition". Proceedings of the IEEE 77 (2): 257–286. doi:10.1109/5.18626. http://www.ece.ucsb.edu/Faculty/Rabiner/ece259/Reprints/tutorial%20on%20hmm%20and%20applications.pdf. [1]
^ Newberg, L. (2009). "Error statistics of hidden Markov model and hidden Boltzmann model results". BMC Bioinformatics 10: 212. doi:10.1186/1471-2105-10-212. PMC 2722652. PMID 19589158. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2722652. edit
^ Wong, W.; Stamp, M. (2006). "Hunting for metamorphic engines". Journal in Computer Virology 2 (3): 211-229. doi:10.1007/s11416-006-0028-7. edit
^ Baker, J. (1975). "The DRAGON system--An overview". IEEE Transactions on Acoustics, Speech, and Signal Processing 23: 24–29. doi:10.1109/TASSP.1975.1162650. edit
^ Jelinek, F.; Bahl, L.; Mercer, R. (1975). "Design of a linguistic statistical decoder for the recognition of continuous speech". IEEE Transactions on Information Theory 21 (3): 250. doi:10.1109/TIT.1975.1055384. edit
^ Xuedong Huang, M. Jack, and Y. Ariki (1990). Hidden Markov Models for Speech Recognition. Edinburgh University Press. ISBN 0748601627.
^ Xuedong Huang, Alex Acero, and Hsiao-Wuen Hon (2001). Spoken Language Processing. Prentice Hall. ISBN 0-13-022616-5.
^ M. Bishop and E. Thompson (1986). "Maximum Likelihood Alignment of DNA Sequences". Journal of Molecular Biology 190 (2): 159–165. doi:10.1016/0022-2836(86)90289-5. PMID 3641921.
^ Richard Durbin, Sean R. Eddy, Anders Krogh, Graeme Mitchison (1999). Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge University Press. ISBN 0-521-62971-3.
^ Ghahramani, Zoubin; Jordan, Michael I. (1997). "Factorial Hidden Markov Models". Machine Learning 29 (2/3): 245–273. doi:10.1023/A:1007425814087.

External links

Concepts

A Revealing Introduction to Hidden Markov Models by Mark Stamp, San Jose State University.
Switching Autoregressive Hidden Markov Model (SAR HMM)
A step-by-step tutorial on HMMs (University of Leeds)
Hidden Markov Models (an exposition using basic mathematics)
Hidden Markov Models (by Narada Warakagoda)

Software

HMMdotEM General Discrete-State HMM Toolbox (released under 3-clause BSD-like License, Currently only Matlab)
Hidden Markov Model (HMM) Toolbox for Matlab (by Kevin Murphy)
Hidden Markov Model Toolkit (HTK) (a portable toolkit for building and manipulating hidden Markov models)
Hidden Markov Model R-Package to set up, apply and make inference with discrete time and discrete space Hidden Markov Models
GHMM Library (home page of the GHMM Library project)
CL-HMM Library (HMM Library for Common Lisp)
Jahmm Java Library (general-purpose Java library)
HMM and other statistical programs (Implementation in C by Tapas Kanungo)
The hmm package A Haskell library for working with Hidden Markov Models.
GT2K Georgia Tech Gesture Toolkit (referred to as GT2K)
Hidden Markov Models -online calculator for HMM - Viterbi path and probabilities. Examples with perl source code.